그래프의 종류
- Directed Graph (방향 그래프) : 간선간에 방향이 존재한다.
- Undirected Graph (무방향 그래프) : 간선간에 방향이 존재하지 않는다.
- Weighted Graph (가중 그래프) : 간선에 weight가 존재한다.
그래프에서 좀더 깊게 들어가면
- Subgraph(부분 그래프) : V' ⊆ V, E' ⊆ E, 그래프에 포함된 그래프
- Complete graph(완전 그래프) : 모든 노드 간에 간선이 연결된 그래프
- Path : 한 노드에서 특정 노드 까지 도착한 노드들의 모임 (simple path는 중복된 노드 도달 불가)
- reachable(도달 가능) : 임의의 노드에서 다른 노드 까지 도달이 가능하다.
- Connected : 모든 vertex가 연결되어 있는 Undirected Graph
- Strongly Connected : Directed Graph에서 모든 vertex가 연결되어 있다.
- Cycle : 출발한 노드로 다시 돌아 올 수 있는 그래프 vs Acycle : 출발한 노드로 다시 돌아오지 못한다.
그래프를 구현하는 방법
- 에지 리스트
- 인접 행렬
- 인접 리스트


에지 리스트
에지 리스트는 edge를 중심으로 그래프를 표현한다. 출발 노드와 도착 노드를 지정하여 에지를 포현한다.

에지 리스트는 표에서도 볼 수 있듯이 특정 노드와 관련되어 에지를 탐색하기는 쉽지 않다. 그래서 에지 중심의 알고리즘인 벨만 포드나 크루스칼 알고리즘에 사용된다.
- 크루스칼 알고리즘 : 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용하는 알고리즘이다. (최소 신장 트리)
- 벨만 포드 알고리즘 : 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. edge의 가중치가 음수일 때도 최단 거리를 구할 수 있다.

디익스트라 알고리즘
- 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하여 한단계씩 최단 거리를 구해나간다.
- 음수 간선이 없을 때 최적의 해를 구할 수 있다.
- 시간 복잡도는 O(ElongV)
벨만 포드 알고리즘
- 매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리를 구한다. (디익스트라 알고리즘에서의 최적해를 항상 포함하게 된다.)
- 음수 간선이 있어도 최적의 해를 찾을 수 있다.
- 시간 복잡도는 O(VE)
인접 행렬
2차원 배열을 자료구조로 이용하여 그래프를 표현한다. 노드 중심으로 그래프를 표현한다.

장점
- 두 노드를 연결하는 에지의 여부와 가중치 값은 배열에 직접 접근하면 바로 확인 할 수 있다.
단점
- 노드와 관련된 edge를 탐색하려면 N번 접근해야 한다.
- 노드 개수에 비해 edge가 적을 때는 공간 효율성이 떨어진다.
- 노드 개수가 많은 경우는 2차원 배열 선언 자체를 할 수 없을 수도 있다.
인접 리스트
ArrayList로 그래프를 표현한다.
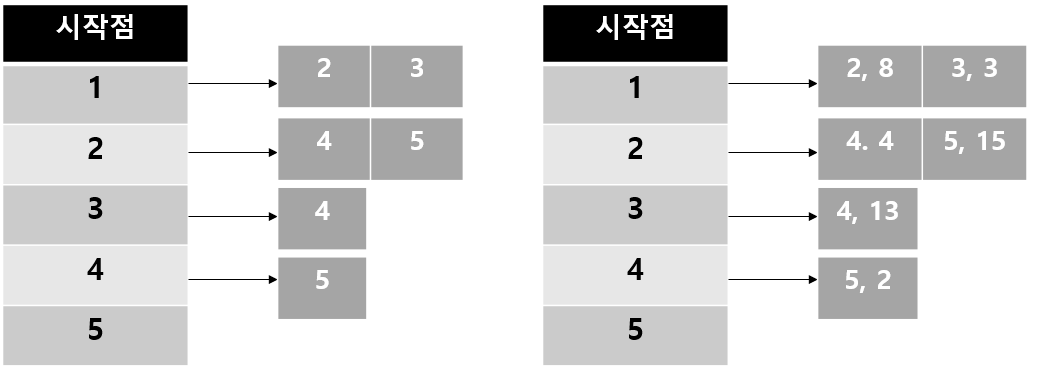
장점
- 노드와 연결되어 있는 에지를 탐색하는 시간이 매우 뛰어나다.
- 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러가 발생하지 않는다.
| 인접 행렬 | 인접 리스트 | |
| 간선 정보를 저장하는 메모리 공간 | O(V^2) | O(E) |
| 특정 2개의 노드가 인접 했는지 (adjacent) |
O(1) | V의 노드 에서 간선의 수 = deg(a) W의 노드에서 간선의 수 = deg(b) O(min(deg(V), deg(W))) -> 무방향 O(deg(V)) -> 방향 그래프 |
| edge와 노드가 연결되어 있는지 검사 (incident) |
O(V) 노드의 수만큼 탐색 | O(deg(V)) |
그래프를 활용한 알고리즘
1. BFS, DFS (그래프 traverling)
2. 서로소 집합(유니온 파인드)
서로소 집합 보러가기
3. 최소 신장 트리 구하기
- 프림의 알고리즘 (그리디 알고리즘으로 최소 신장 트리 구하기) O(ElogV)
- 크루스칼의 알고리즘 (유니온 파인드를 사용해 최소 신장 트리 구하기) O(ElogV) 간단하게 설명하자면 가중치를 기준으로 edge를 오름차순으로 정렬 한 뒤 작은 수 부 터 탐색하면서 cycle만 없게 탐색하는 것이다. cycle이 있는지 없는지 검사할 때, 유니온 파인드가 사용된다.
4. 최단 거리 구하기
- 디익스트라 알고리즘
- 벨만 포드 알고리즘
- 플로이드 워셜 알고리즘 (모든 노드간의 최단 거리 구하기)
5. 위상 정렬
사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘이다. 시간 복잡도는 O(V+E)
위상정렬 보러가기
6. 강한 연결 요소 추출 알고리즘
- 코사리주 알고리즘 (DFS를 2번 하여 강한 결합 요소를 찾는다)
- 타잔 알고리즘 (DFS를 한번만 수행해 강한 결합 요소를 찾는다) 코딩 테스트에서 이 알고리즘이 더 많이 쓰인다.
강한 결합 요소 보러가기
'BackEnd > 알고리즘 공부' 카테고리의 다른 글
| 위상정렬, 줄 세우기(백준_2252) (0) | 2023.01.24 |
|---|---|
| 유니온 파인드, 집합의 표현(백준_1717) (0) | 2023.01.22 |
| 사탕 가게(백준_4781) (0) | 2023.01.20 |
| 합이 0인 네 정수(백준_7453번) (0) | 2023.01.15 |
| 빙산(백준_2573) (0) | 2023.01.13 |